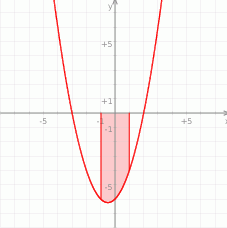
W tym poście przedstawię pokrótce funkcję kwadratową(inaczej trójmian kwadratowy).
Najważniejsza postać funkcji kwadratowej to postać ogólna
ax2+bx+c, przy czym a jest różne od 0, bo wtedy otrzymujemy wzór funkcji liniowej
Drugą postacią trójmianu kwadratowego jest postać iloczynowa
a(x-x1)(x-x2) , gdzie
x1 i
x2 są rozwiązaniami funkcji kwadratowej.
Trzecią postacią trójmianu kwadratowego jest postać kanoniczna, która jest oparta na współrzędnych wierzchołka. Współrzędna x-owa(p) wierzchołka to
-b/2a, a y-owa(q) to
-(b2-4ac)/4a delta=(b
2-4ac)
Tak więc postać kanoniczna funkcji kwadratowej to nic innego niż przesunięty wykres ax
2 o wektor [p,q], a więc postać ta wygląda tak
a(x-p)2+q

Własności
Funkcja kwadratowa ma kształt paraboli, dlatego zawsze ma nieskończony zbiór wartości
Jest symetryczna względem prostej x o równaniu x=p
Ma dwa pierwiastki rzeczywiste, gdy wyróżnik jest dodatni, jeden, jeśli delta=0 i 0 rzeczywistych( dwa zespolone), gdy delta<0
Ma ramiona skierowane do góry, gdy a>0, a gdy a<0 to do dołu
Wzory Viète'a
Dla równania kwadratowego, które posiada pierwiastki x1 i x2 (działają również dla pierwiastków zespolonych):
* x1+x2= -b/a
* x1*x2= c/a

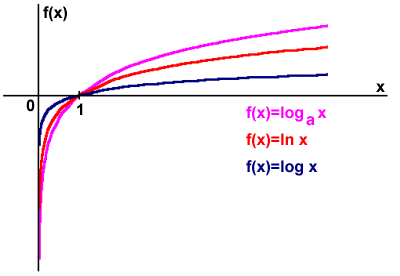
,_y%3Dlog3%5E-1(x).png/400px-Wykres_y%3Dlog2%5E-1(x),_y%3Dlog3%5E-1(x).png)