a2+b2 ≥ 1/2
a3+b3 ≥ 1/4
1 Stosujemy wzór skróconego mnożenia dla wyrażenia a+b=1
(a+b)2=1
a2+2ab+b2=1
a2+b2=1-2ab
Zauważmy, że 2ab=2a(1-a)=-2a(a-1)=-2a2+2a i największa wartość tego wyrażenia wynosi -(22-4*(-2)*0)/(4*(-2))=-4/-8=1/2 wobec tego 2ab≥1/2, czyli
a2+b2≥1-1/2=1/2
2 Stosujemy wzór skróconego mnożenia dla wyrażenia a+b=1
(a+b)3=a3+3a2b+3ab2+b3=a3+b3+3ab(a+b)
a3+b3+3ab(a+b)=1
a3+b3+3ab=1
Korzystając z 2ab≥1/2 mamy 2ab≥1/2 |:2
ab≥1/4 |*3
3ab≥3/4, czyli
a3+b3=1-3ab≥1-3/4=1/4

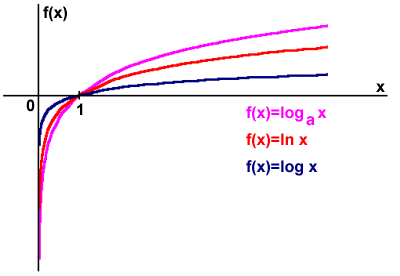
,_y%3Dlog3%5E-1(x).png/400px-Wykres_y%3Dlog2%5E-1(x),_y%3Dlog3%5E-1(x).png)